Four mice are initially sitting at the corners of a unit square. At the same time, each of the mice begin running with equal speed directly toward the mouse on their right. How far do the mice travel?

Consider the mouse beginning at the origin, which we chose to be bottom left corner of the square, once she has travelled some way along the path. At this point, the mouse to her right has travelled along the same path but rotated 90 degrees counter clockwise.
We can use the symmetry of the situation to find a derivative using some geometry, which will help us determine the shape of the mouse’s path.
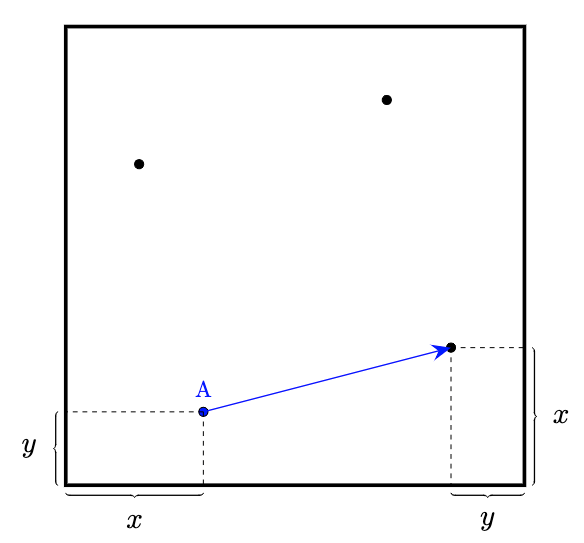
We will focus on the mouse at point A. The slope of the blue line is the rise over the run, so we find the derivative
We can consider this a differential equation to solve for , the path of the mouse. However, this looks like a slightly intractable non-linear equation.
We’ll perform the common maths trick of (seemingly) making the problem look harder in order to make progress. We can use the power of the chain rule to introduce a new variable, , which we can consider to be the time after the mouse’s journey begins, and note that
We can now break this into two separate equations,
This is a system of two equations in and
, but crucially they are now first order linear differential equations.
Let’s use Laplace Transforms to solve this system of equations. Define the transforms and
, then the system transforms into
Since this particular mouse begins at the origin, we have and
. Solving the system of now algebraic equations we find that
Performing some Partial Fraction Decomposition, we can write these as
Inverting the transforms we obtain parametric equations for the mouse’s path
While we could trace out the path as defined above, we know that the mice have velocity vectors that are perpendicular at any point in time, and so we can get an idea by simply looking at squares that have been scaled and rotated. These images are sometimes called “whirls”, curves created by a series of straight lines.

How far does the mouse travel? The journey will take an infinite amount of time, as our mice spiral towards the centre of the square, but we can still calculate the total distance using the arc-length formula,
Since and
the total distance travelled is
the same distance as the side length of the square.
The extension of this problem to other regular polygons is quite natural, and makes for some pretty animations, which I stole from Wolfram Mathworld.
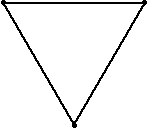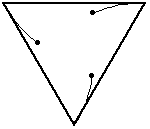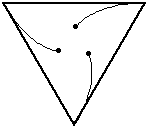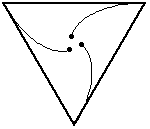

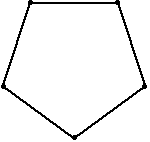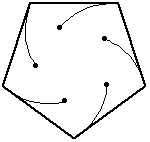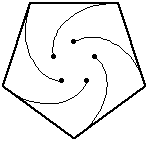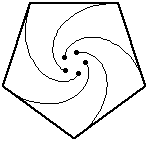
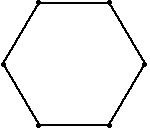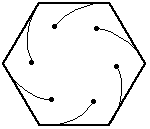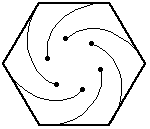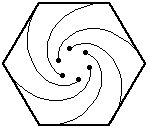
In general, for a regular polynomial with sides, the mice each travel a distance
If you’re interested in these extensions and the use of Laplace transforms, here is a very thorough student report covering both.

Leave a comment