The Calculus of Explanations

When I used to teach maths to mechanical engineers, one lecture I used to particularly enjoy was related to Moment of Inertia, the property of a body that measures its ability to resist changes to its angular velocity.

Galileo discovered that objects fall at the same rate under gravity, regardless of their mass (ignoring air resistance). But why? Shouldn’t heavier things fall faster? Newton’s Law of Gravity says the attractive force between an object of mass and the earth, of mass a distance apart is

so the bigger the mass , the larger the force and therefore acceleration, right?

Not quite! We have to remember Newton’s first law, which tells us about inertia, the property of mass to resist changes in its motion. The degree to which this occurs when an object falls to earth is what we call the mass of the object. Newton’s second law tells us that

and the larger force we saw before is exactly balanced by the larger mass! So the acceleration remains the same as for a less massive object.

More massive objects weigh more, because the attraction force to the planet is higher, but they’re also harder to pull, because they have a higher inertia, and thus resist motion more. 

What about objects rolling down an inclined plane (ignoring friction)? Do they fall at the same rate too? Well… it depends.

You may think that the speed an object rolls down an inclined plane might depend on its mass (in contrast to falling objects), or at least on its radius. In fact, the speed an object rolls depends only on the distribution of its mass.

To explain further, let’s have a race!

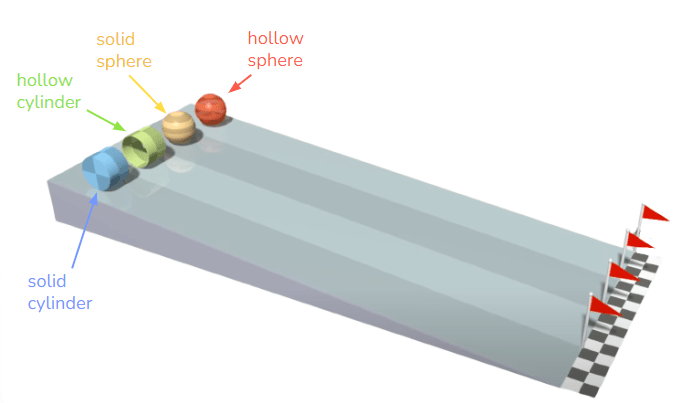
Let’s take mass and radius out of the equation, just in case you don’t believe me. A solid cylinder, a hollow cylinder, solid sphere and a hollow sphere, all of the same mass and cross-sectional radius, are going to roll down a hill. Who wins? Or maybe you think it’s a two way tie, or even a four way tie?

Quick, say your answer out loud so I know you’re not cheating!

I have asked this question of a group of a dozen very intelligent people, most of them with a maths degree, and the answers varied wildly:

Hollow cylinder (5)
Solid objects tied first (3)
Spheres tied first (1)
Cylinders tied first (1)
Solid sphere (1)

This tells us two things, that the answer isn’t particularly intuitive, and that it’s not something typically taught in mathematics courses.

Let’s see the results!

The placings are

1. solid sphere
2. solid cylinder
3. hollow sphere
4. hollow cylinder

The solid sphere wins! The next posts in this series will be dedicated to explaining why the race went the way it did.