The Calculus of Explanations

Putting the fun in functionals

Moments of Inertia – Part III

There are some very useful theorems that can help in evaluating Moments of Inertia.

Parallel Axis Theorem

The first is the Parallel Axis Theorem. This theorem states that if you know the MOI for rotation about one axis, then the MOI for rotation around a different but parallel axis differs by Md^2, where M is the mass of the object and d the distance between the axes.

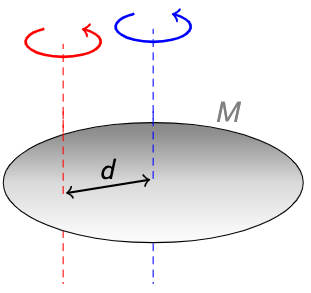
That is, if the axis \Gamma' is parallel to axis \Gamma , then

I_{\Gamma'} = I_{\Gamma} + Md^2.

This helps since it is often hard to calculate MOI using the integral definition, unless the axis passes through the object’s centre of mass.

Example

Consider the example of a solid sphere on the end of a rod, rotating around an axis at the end of the rod.

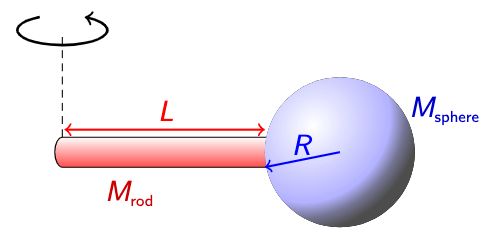
By the principle of superposition and the parallel axis theorem,

\begin{aligned} \displaystyle I &= I_{\text{rod about end}} + I_{\text{sphere about centre}} + I_{\text{parallel axis contribution}}\\ I &= \frac{M_{\text{rod}}L^2}{3} + \frac{2M_{\text{sphere}}R^2}{5} + M_{\text{sphere}}(L+R)^2 \end{aligned}

Perpendicular Axis Theorem

The second theorem is the Perpendicular Axis Theorem.

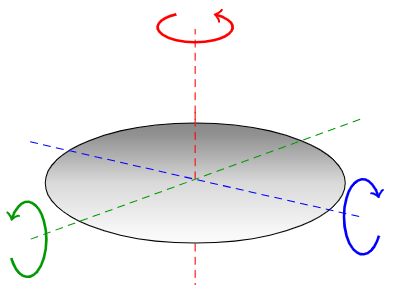
For a thin object in the x–y plane, the MOI about the z axis, perpendicular to the plane, is the sum of the MOI in the x direction and y direction. Since

I = \displaystyle \int r^2 \ \mathrm{d}m = \int y^2 \ \mathrm{d}m + \int x^2 \ \mathrm{d}m

we have

I_{z} = I_{x} + I_{y}

Example

Find the MOI of a disk with mass M and radius R lying in the x–y plane, being rotated about the x axis.

By the perpendicular axis theorem,

I_z = I_x + I_y

and we know that I_z = MR^2.

By symmetry I_y = I_x, so

I_z = 2I_x

and rearranging we get that

\boxed{I_x = \displaystyle \frac{MR^2}{4}}

In the next post in this series, we will investigate using symmetry in a different way, by using the method of self-similarity to find moments of inertia.

OnNumbersandGames's avatar

Posted by:

OnNumbersandGames

Leave a comment

Hi there! I’m a content creator with a background in maths education and a passion for making complicated ideas simple, with intuitive animations and visual explanations.

Whether you’re just entering high school or you’re a post-grad student, or just have an interest in maths in general, I aim to make content that can appeal to everyone, in the form of videos and blog posts.

You can find all my previous posts here.

Check out my YouTube channel for more maths education content.

Recent Posts