Moments of Inertia – Part IV – The Calculus of Explanations

In this post, we explore the method of self-similarity for calculating Moments of Inertia.

An analysis of the units shows that the MOI is always proportional to $M L^2$ where $M$ is the total mass of the object and $L$ is some representative length scale.

Calculating the MOI from the integral definition for any but the simplest objects can be quite challenging. However, if the object in question has the property of self-similarity then we can calculate the MOI with no integration necessary.

Since $I = \gamma M L^2$ , where $\gamma$ is a constant of proportionality, if we can construct a similar shape using several copies of the original shape, we can use the parallel axis theorem to solve for the MOI.

Example – An equilateral triangle

To find the MOI of an equilateral triangle of side length $L$ and mass $M$ , being rotated about a central axis, we can exploit its rotational symmetry and the use the principle of self-similarity, surrounding the original triangle (in white) with three copies of itself (in red).

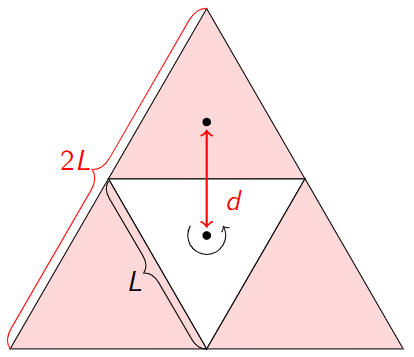
This process creates another equilateral triangle, which has been scaled up in length by a factor of two, and therefore in area (and therefore mass) by a factor of four.

Since $I=\gamma ML^2$ for some $\gamma$ ,

$I_{\text{big}} = \gamma (4M)(2L)^2 = 16I$

Using the principle of superposition,

$I_{\text{big}} = I + 3 I_{\text{edge}}$

Using the parallel axis theorem,

$I_{\text{edge}} = I + Md^2$

where $d = L/\sqrt{3}.$ Hence

$16I = I + 3\left(I + \frac{ML^2}{3}\right) ,$

and we find that

$\boxed{I = \displaystyle \frac{ML^2}{12}}$

Example – A Square

Finding the MOI of a square using integration is actually quite simple, however to further illustrate the self-similarity method, we can surround a square with eight identical copies of itself.

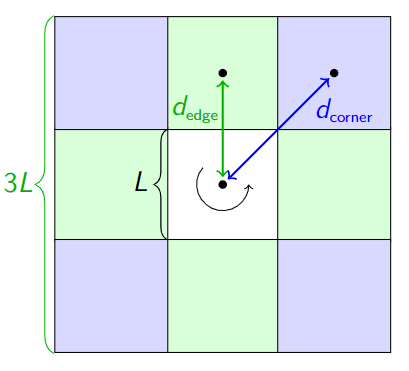
Note that there are now both edge (green) and corner cases (blue) to consider. Repeating the trick from before,

$I_{\text{big}} = \gamma (9M)(3L)^2 = 81I$

Using the principle of superposition, noting that the large square contains 4 edge copies and 4 corner copies,

$I_{\text{big}} = I + 4I_{\text{edge}}+ 4I_{\text{corner}}.$

Now, using the parallel axis theorem we have

$I_{\text{edge}} = I + Md_{\text{edge}}^2,$

where $d_{\text{edge}} = L$ , and

$I_{\text{corner}} = I + Md_{\text{corner}}^2,$

where $d_{\text{edge}} = \sqrt{2} L$ . Putting these pieces together,

$81I = I + 4(I+ML^2) + 4(I+2ML^2),$

and we get the final result that

$\boxed{I =\displaystyle \frac{ML^2}{6}}$

This technique can easily be extended to find the MOI of a rectangle, and both results should be straightforward to confirm using the integration approach.

In the next and final part in this series, we will stretch the method of self-similarity to its limit in order to find the moments of inertia for more exotic shapes in the plane.

The Calculus of Explanations