The Calculus of Explanations

A slightly impractical but fascinating use of the self-similarity method is finding the Moment of Inertia of certain famous fractals.

Example – The Sierpiński Triangle

Consider that the Sierpiński triangle of mass and side length is comprised of three smaller copies of itself.

If the triangle is being rotated about its centre, we simply need to calculate between to the centre of one of the smaller constituent triangle.

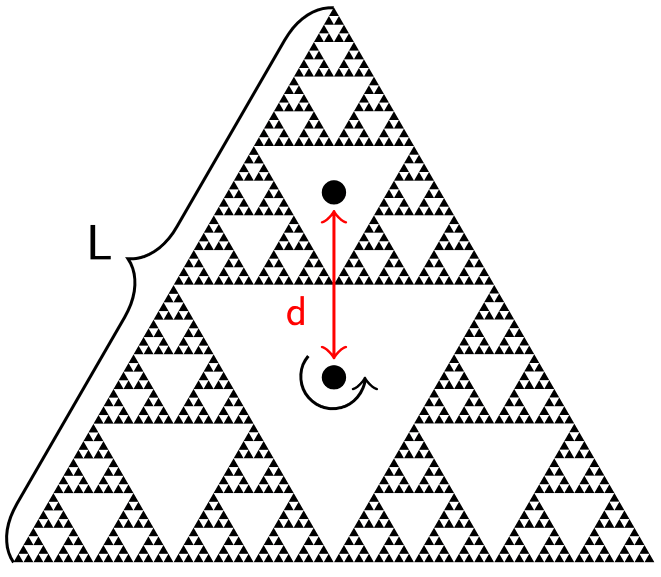
So

Using the Parallel Axis Theorem,

where

the contribution of each small triangle is the moment of inertia through its centre of mass (COM) plus its mass multiplied by the distance to the axis of rotation squared. This distance is , so we find that

With which we reach the final result

Note that the moment of inertia is larger than the MOI of an equilateral triangle with equivalent mass, which was , since in the fractal more of the mass is distributed far away from the axis of rotation!