The Calculus of Explanations

A few years ago I watched the brilliant Numberphile video with Simon Pampena about using circle inversion to solve a problem involving Pappus’ chains, also known as Appolonian gaskets.

Although the presentation was compelling and the problem interesting, it was a bit complicated and long for a first introduction to the topic.

I started playing around with this technique and tried to find simple examples I could use to demonstrate the power and ease of using circle inversion to solve problems in geometry.

As an aside, I was interested to learn that the Japanese seemed to like these types of tangency problems, see theSangaku problems which were “placed as offerings at Shinto shrines or Buddhist temples during the Edo period by members of all social classes.”

The first problem I chose was to find the radius of the circle below. Note the large amount of tangency in the problem. The circles are tangent to each other, and the inner circles are tangent to the diameter of the unit circle.

This high degree of tangency in the problem makes it a great candidate for using circle inversion, in the same way the original Appolonian gasket was – circle inversion is a conformal map, so angles are preserved under the transformation. Inversion is a specific conformal map that preserves the shape of circles (not just infinitesimally small circles but all circles!)

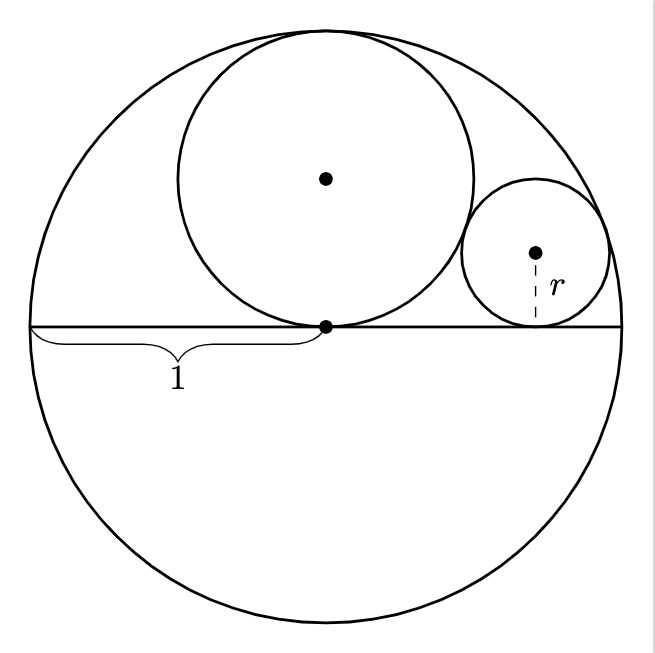
These two properties mean that the circles that are tangent in the original problem become, under inversion, circles that are tangent to each other in the inverted space.

Not only that, circles that go through the origin of the inversion circle end up as straight lines in the inverted space (or circles of infinite radius).

Hence the inverted problem often becomes easier to solve than the original problem. This is the key for using any transformation technique in mathematics. We have a “difficult” problem we wish to solve, but the transformation turns it into an “easy” problem. As long as we have a way to convert the solution back to the original context (an inverse transformation), we can obtain the solution to the original problem. Circle inversion is simple in this respect as well, since applying the inverse transform is the same level of difficulty as the transform itself.

This first problem, combined with the boredom of lockdowns during the pandemic in 2020, along with a little extra motivation provided by Grant Sanderson (of 3 Blue 1 Brown fame) and his inaugural Summer of Maths Exposition (SoME), led to the first video on my YouTube channel.

In it, we talk about transformations in the plane generally, introduce the circle inversion transformation, then solve the problem above.

I then found a second problem from the Art of Problem Solving site, which came complete with a solution. However, the solution shown uses a circle of inversion that is not present in the original problem! Elegant, but perhaps not intuitive. I came up with an approach more along the lines of the first problem, and the second video in the series is finally up.

My clickbait title (for the time being anyway) is Zero Trigonometry Required, since circle inversion gives us a fun way of solving problems we’d normally have to use trig to solve.

As a bonus, we solve the problem using Descartes’ Kissing Theorem, described using a poem by Nobel laureate in chemistry Frederick Soddy (1936), and talk about extensions of circle inversion like iterated inversion (fractals), spherical inversion in 3D, and the extension to Mobiüs transformations and how they relate to projective geometry!

Hopefully you enjoyed this little journey through a somewhat obscure topic, and can connect it to some of the maths you’re learning (complex analysis, projective geometry, algebraic topology), or keep it mind next time you encounter a problem in planar geometry that involves circles and lines.

I may return to this topic and playlist in the future, so let me know if you have any suggestions for a follow-up third video on this topic.

Stay curious.