This adventure started when I attempted a harmless looking problem from the Facebook group “Actually Good Maths Problems”. The answer, which any motivated high school calculus student could find, is a sort of joke or prank on the solver, and I enjoyed it enough that I sent the problem to my good friend David Galea.
I thought that would be the end of it.
But then, as mathematicians often do, we started asking each other questions. This lead us down a rabbit hole as the problem morphed into an intriguing riddle with surprising results, which we still haven’t fully understood.
Let’s get into it.
Draw two parabolas, and the same parabola shifted up one unit,
. Construct a tangent line somewhere on the upper parabola at a general point
, and consider the area bounded below by the tangent, and above by the bottom parabola
.
The problem is to find the tangent point that maximises this area, and to find that maximal area.
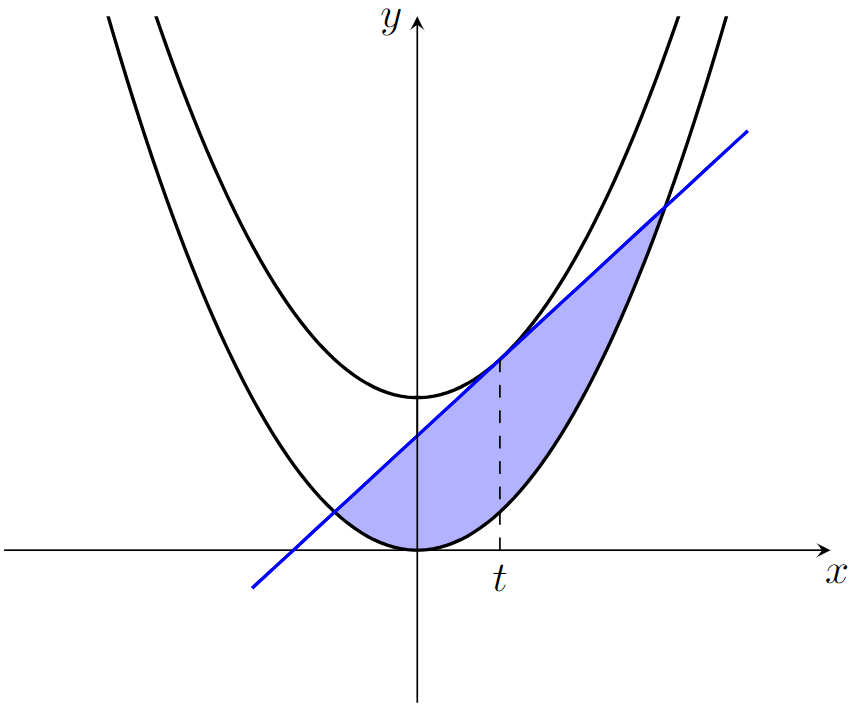
Noting that the derivative for the curve evaluated at the tangent point is
, and that the tangent goes through the point
, the formula for the tangent line is given by
or, simplifying,
The area between this tangent and the lower parabola is now a function of this parameter (subtract the bottom curve from the tangent line and integrate):
where and
are the left and right intersection points respectively, i.e. the two solutions of
This is a quadratic, with the solutions , so
and
, since the left intersection point has to be smaller than the right.
Now, we have an expression for , the area we are trying to maximise. So we have to take a derivative with respect to
. We could try to evaluate the integral first, but it’s easier and more interesting to use Liebniz’s rule for differentiating integrals (we need this, since the limits themselves depend on
). If we let the integrand be
, then
It’s not too hard to show that , and the integral also evaluates to
.
Thus we have the fact that and therefore, the area under the curve is a constant, independent of
!
If we let , then we can see that the area is
So we have our answer. The area is the same no matter where we place the tangent, and it’s .
As I said, a mildly amusing result. Don’t believe it? Try it here, drag the tangent point and see the area remain the same.
The next chapter in the story was David and I wondering whether the area was also constant when we generalise the problem to higher dimensions.
What we found was extremely surprising, I hope you’ll join us to explore this problem further in the next post.
Stay curious!

Leave a reply to A problem of paraboloids – The Calculus of Explanations Cancel reply